Coefficient de performances d'une pompe à chaleur (COP)

Une bonne compréhension des machines thermiques passe par l’étude du cycle de Carnot.

Ce cycle étudie les échanges thermiques d’un fluide parfait entre deux isothermes et deux adiabatiques. (Voir figure ci-dessous)

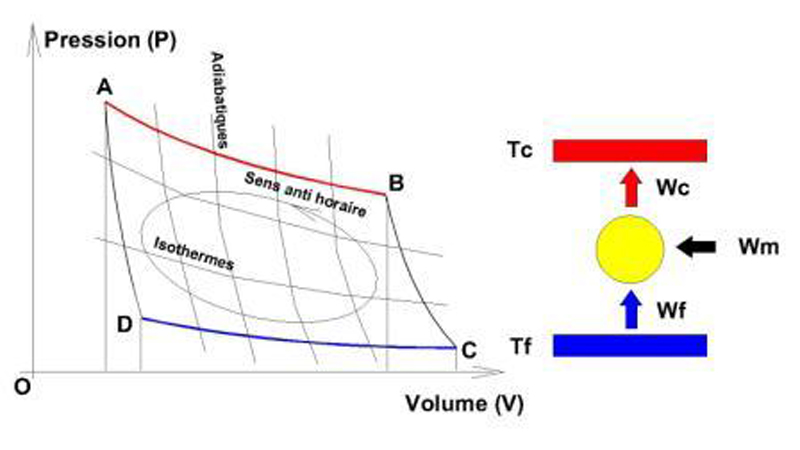
Le cycle peut se dérouler dans le sens horaire ou inversement. La surface comprise entre ces 4 courbes représente l’énergie mécanique Wm que la machine produit ou reçoit.

- Lorsque le cycle se déroule dans le sens horaire, la machine thermique classique (locomotive à vapeur ou  centrale thermique) transforme en énergie mécanique un pourcentage de l'énergie thermique transportée de la source chaude vers la source froide égal, idéalement, à 100 x (T_c - T_f) / T_c appelé improprement rendement théorique maximum.

- Lorsque le cycle se déroule dans le sens antihoraire la machine thermique fonctionne alors en machine frigorifique (pompe à chaleur) et l'énergie thermique est transportée de la source froide vers la source chaude. Pour assurer le déroulement du cycle, la pompe à chaleur reçoit de l'énergie mécanique (en pratique le compresseur délivrant cette énergie est le plus souvent entraîné par un moteur électrique).

Lien vers un site explicatif

Considérons la machine thermique dans ce dernier cas. Avec des températures en °F aux sources chaudes et froides suivantes      T_c    température source chaude, T_f    température source froide On a  d’après l’équation des gaz parfaits  

Wc = P_cV_c = RT_c et Wf = P_fV_f = RT_f   où  R est la constante universelle des gaz parfaits (8,314 472 J·K^-1·mol^-1)

Le principe de la conservation de l'énergie permet d'écrire que Wc = Wm + Wf

(En d'autre terme au cours d'un cycle, l'énergie thermique envoyée par la pompe à chaleur vers la source chaude est égale à celle reçue par celle-ci en provenance de la source froide majorée de l'énergie mécanique nécessaire à l'élaboration du cycle)

L’énergie mécanique fournie par le compresseur est  donc égal à Wm = Wc - Wf =  P_cV_c - P_fV_f = R (T_c - T_f)

Et le COP représentatif du rendement de la pompe à chaleur  est égal à   COP = P_cV_c / Wm  =  T_c / (T_c - T_f)

COP = T_c / (T_c - T_f)

Application numérique dans le cas de l'aquathermie lorsque la température de la source chaude Tc varie

Calcul théorique effectué pour une température donnée à la source froide de T_f = 10 °C  (ou 283K)
On constate que le rendement de la machine thermique change selon la température à la source chaude T_c

Température source chaude Tc
Centigrades	Kelvin	COP théorique
30°C	303K	15,2
40°C	313K	10,4
50°C	323K	8,1
60°C	333K	6,7

La théorie des gaz parfaits conduit à des résultats optimistes qui ne sont malheureusement pas atteint dans la pratique.

Les COP réels tenant compte des imperfections du cycle sont plus faibles.

Le rendement réel est probablement affecté par une mauvaise isolation, des frottements, le fait que les deux transformations dites adiabatique ne le sont pas totalement, le mode de régulation adopté pour la pompe à chaleur. Toutes ces raisons peuvent expliquer pourquoi les COP obtenus dans la réalité sont sensiblement divisés par deux.  Les résultats ci-dessus obtenus à partir de la formule  COP = 1/(1-1/(Tc/Tf)  = Tc / (Tc - Tf) corroborent sensiblement ceux diffusés par l'Ademe.

Ces résultats  mettent en évidence une amélioration du COP lorsque la température de la source chaude  se rapproche de celle de la source froide

Le diagramme de Mollier

Les 2 figures ci-dessous permettent aussi de mieux comprendre le fonctionnement d'une pompe à chaleur.

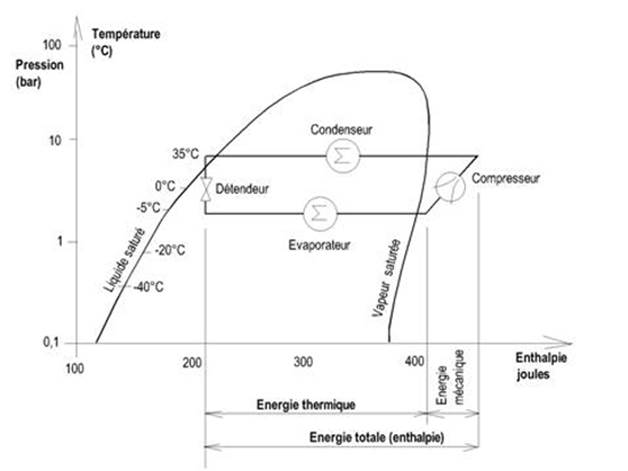
Lorsque la température de la source chaude (condenseur) est proche de la température de la source froide (évaporateur),

l’énergie mécanique fournie par le compresseur est plus faible et le COP (énergie thermique délivrée par le condenseur / énergie mécanique) est plus élevé.

En raison du principe de la conservation de l’énergie, l'énergie totale (enthalpie) est égale à la somme des énergies frigorifique de l’évaporateur et mécanique

La bonne cohabitation des deux fluides gaz et électricité permet d’améliorer le COP et de réduire les frais d’exploitation

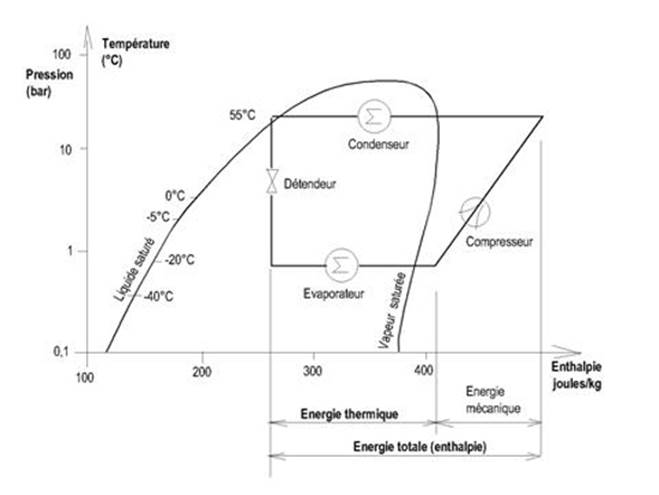
Lorsque la différence entre la température de la source chaude (condenseur) et celle de la source froide (évaporateur) augmente,

l'énergie mécanique fournie par le compresseur augmente également et le COP (énergie frigorifique / énergie mécanique) est moins bon.

Voir le livre
"Les pompes à chaleur "
de Bruno Béranger des éditions Eyrolles  (2ème édition)

La figure ci-dessus donne une idée des rendements que l'on peut  escompter avec une pompe à chaleur moderne en fonction des températures d'évaporation (température de la source froide) et les températures de condensation (température de la source chaude)

- La partie gauche de l'abaque correspond aux pompes à chaleur aérothermiques.  Une croissance importante est prévue pour cette solution dans la rénovation et à un degré moindre dans le collectif. Plus simple et proche des systèmes de climatisation traditionnelle, elle est souvent utilisée dans les pays méditerranéens en chauffage individuel et depuis peu en collectif.

- La partie centrale correspond aux pompes à chaleur géothermiques. Les échanges thermiques se font avec le sol. Le nombre de forages va en diminuant s’il y a un peu d’eau dans le sous-sol mais il reste important augmentant l’investissement initial.

-  La partie droite correspond aux pompes à chaleur aquathermiques sur nappe libre. Plus coûteuses à l'installation que les pompes à chaleur aérothermiques, elles restent intéressantes dans le cas d'un immeuble par le fait que les frais du forage de l’exhaure et du rejet sont répartis sur un grand nombre de copropriétaires. Très intéressantes en terme de frais d'exploitation elles s'insèrent mieux dans l'ancien et la rénovation que les pompes aérothermiques